大家好，这是我们翻译的西瓜书平替。

「小白学 AI 该从哪里下手？」

去互联网上搜索一圈，最高赞的回复往往是高数起手，概率论也要学一学吧，再推荐一本大名鼎鼎的「西瓜书」。

但入门的门槛足以劝退一大波人了。翻开《西瓜书》前几页，看看基本术语解释，一些基本数学概念还是要了解的。

西瓜书《机器学习》第 3 页。

但为了避免「从入门到放弃」，有没有一种可能，不需要学更多数学，就能搞懂大模型的运行原理？

最近，Meta Gen AI 部门的数据科学总监 Rohit Patel 听到了你的心声。他用加法和乘法 —— 小学二年级的数学知识，深入浅出地解析了大模型的基础原理。

原文链接：https://towardsdatascience.com/understanding-llms-from-scratch-using-middle-school-math-e602d27ec876

如果你想更进一步，按照博客中的指导，亲手构建一个像 Llama 系列的 LLM 也完全可行。

读过的网友留下了好评：「博客相当长，虽然我才看了一半，但可以向你保证，这值得花时间一读。」

「所有的知识点都包圆了，学这 1 篇顶 40 亿篇其他资料！」

内容概览

为了使内容更简洁，Rohit 尽量避免了机器学习领域的复杂术语，将所有概念简化为了数字。

整个博客首先回答了四个问题：

在基础的原理摸清之后，Rohit 要从细节入手，从嵌入、分词器、自注意力等概念讲起，由浅入深，逐步过渡到对 GPT 和 Transformer 架构的全面理解。

这个博客对新手有多友好呢？先来试读一段：

神经网络只能接受数字输入，并且只能输出数字，没有例外。关键在于如何将各种形式的输入转换为数字，以及如何将输出的数字解读为所需的结果。从本质上讲，构建 LLM 的核心问题就是设计一个能够执行这些转换的神经网络。

那么一个可以根据图片输入，分出花朵和叶子的神经网络大概是这样的：

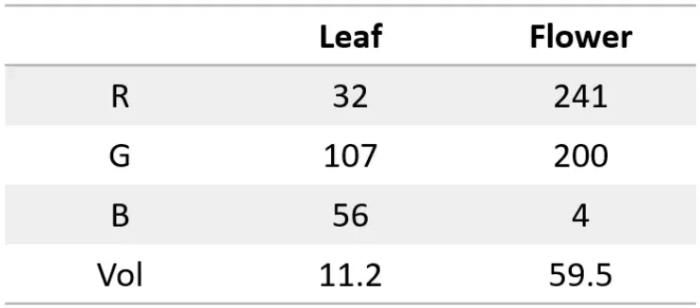
其中，RGB 值表示图像的颜色信息，Vol 则表示图像中物体的尺寸

神经网络无法直接根据这些数字分类，为此，我们可以考虑以下两种方案：

由于「双输出」的方法在后续的步骤中更通用，一般都会选择这种方案。

以下是基于「双输出」的神经网络分类结构，让我们逐步分析其工作原理。

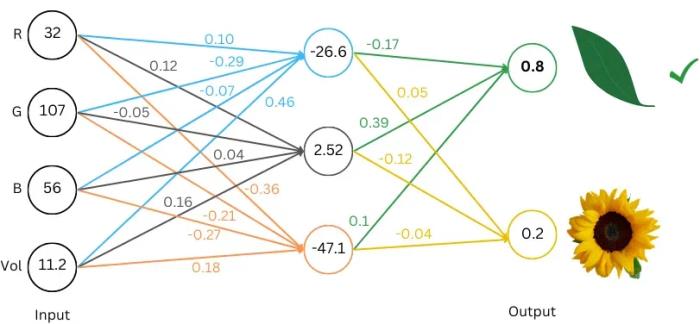
图中圆圈内的数值代表：神经元 / 节点。连接线上的有色数字代表权重。每一列代表一层：神经元的集合称为一层。可以将该网络理解为具有三层：输入层（4 个神经元）、中间层（3 个神经元）和输出层（2 个神经元）。

那么中间层的第一个节点的计算如下：

(32 * 0.10) + (107 * -0.29) + (56 * -0.07) + (11.2 * 0.46) = -26.6

要计算该网络的输出（即前向传播过程），需要从左侧的输入层开始。我们将已有的数据输入到输入层的神经元中。接着，将圆圈内的数字乘以对应的权重，并将结果相加，依次传递到下一层。

运行整个网络后，可以看到输出层中第一个节点的数值较大，表示分类结果为「叶子」。一个训练良好的网络可以接受不同的 (RGB, Vol) 输入，并准确地对物体进行分类。

模型本身并不理解「叶子」或「花朵」是什么，也不了解 RGB 的含义。它的任务仅仅是接收 4 个数字并输出 2 个数字。我们负责提供输入数值，并决定如何解读输出，例如当第一个数值较大时，将其判断为「叶子」。

此外，我们还需要选择合适的权重，以确保模型在接收输入后给出的两个数值符合需求。

我们可以使用相同的网络，将 (RGB, Vol) 替换为其他数值，如云量和湿度，并将输出的两个数值解读为「1 小时后晴」或「1 小时后雨」。只要权重调整得当，这个网络可以同时完成分类叶子 / 花朵和预测天气两项任务。网络始终输出两个数字，而如何解读这些数字 —— 无论是用于分类、预测，还是其他用途 —— 完全取决于我们的选择。

为了尽可能简单，刚刚的「神经网络」中省略了以下内容：

激活层：在神经网络中，激活层的主要作用是引入非线性因素，使网络能够处理更复杂的问题。如果没有激活层，神经网络的每一层只是对输入进行简单的加法和乘法运算，整体上仍然是线性的。即使增加多层，这样的网络也无法解决复杂的非线性问题。

激活层将在每个节点上应用一个非线性函数，常用的激活函数之一是 ReLU，其规则是：如果输入是正数，输出保持不变；如果输入是负数，输出为零。

如果没有激活层，上一个例子中的绿色节点的值为 (0.10 * -0.17 + 0.12 * 0.39–0.36 * 0.1) * R + (-0.29 * -0.17–0.05 * 0.39–0.21 * 0.1) * G，所有中间层就像摊大饼一样铺在一起，计算也将越来越繁复。

偏置：在神经网络中，每个节点（也称为神经元）除了接收输入数据并进行加权求和外，还会加上一个额外的数值，称为偏置。偏置的作用类似于函数中的截距。在模型中我们又称它为参数。

例如，如果顶部蓝色节点的偏置为 0.25，则节点的值为：(32 * 0.10) + (107 * -0.29) + (56 * -0.07) + (11.2 * 0.46) + 0.25 = -26.35。

通过引入偏置，神经网络能够更好地拟合数据，提高模型的表现。

Softmax：Softmax 函数用于将模型的输出转换为概率。它可以将任何数转换为一个范围在 0 到 1 之间的数，且所有元素之和为 1。这使得每个输出值都可以转化为对应类别的概率。

更多研究细节，请参看博客原文。

作者介绍

这篇博客的作者 Rohit Patel 在数据科学领域深耕了 15 年，现在是 Meta GenAI 数据科学总监，参与了 Llama 系列模型的研发。

Rohit 拥有跨越多个领域的丰富职业经历。他的职业生涯始于 2002 年，在 Brainsmiths Education 担任物理助教。随后，他在金融领域从业十年。

2018 年，他加入了 Meta，担任 Facebook Monetization 的数据科学总监。2020 年，他创立了 CoFoundUp，担任创始人兼首席执行官。2021 年，他又创办了 QuickAI，QuickAI 是一款专注于简化数据科学流程的可视化工具，用户无需安装任何应用程序、插件或扩展，即可在浏览器中完成数据科学任务。

参考链接：

https://x.com/rohanpaul_ai/status/1854226721530073162

https://towardsdatascience.com/understanding-llms-from-scratch-using-middle-school-math-e602d27ec876