欢迎来到「带注释的 GPT-2」。

我读过的最精彩、解释最清楚的文章之一是「The Annotated Transformer」。它引起了前所未有的关注，一个简单的想法就是用一个文件注释你所需要的代码。

我在机器学习方面的经验让我意识到，当你将事情写成代码的时候，其实现和秘密会变得更清晰，而不再是魔法了。

魔法没有什么神奇的。魔术师只是理解一些简单的东西，而这些东西对未经训练的观众来说似乎并不简单。一旦你学会了操作魔术卡片，你也可以变魔术。

——Jeffrey Friedl 在《Mastering Regular Expressions》一书中写道

GPT-2 一开始看起来像是魔术，它的看起来太美丽了，但希望我能为你解释魔术，在你读完这篇文章时揭示所有的技巧，这是我的目标。使那些热衷于理解 GPT-2 模型是如何工作的人更好理解。

注：几乎所有代码都是从Hugging Face的 GPT-2 实现中复制、启发和引用的，只保留了简单的基本要素。如果你想在并行 GPU 上训练 GPT-2 模型，在微调时保存检查点，在多个 CPU 上运行推理任务等等，我建议你使用 Hugging Face API。最近，Hugging Face 发布了一个简单的教程，它教你如何做到这一点：

在这篇文章中，我并不是在试图重新发明轮子，而是仅仅把一系列已经存在的优秀资源放在一起，让读者更容易掌握 GPT-2。我让读者在他们所选择的任何领域进一步建立这些基础。

你不能在弱小的基础上建造一座伟大的建筑。如果你要有一个强大的上层建筑，你必须有坚实的基础。

——Gordon B. Hinckley

学习本教程的先决条件

另一个关于 GPT-2 本身的优秀资源，是 Jay Alammar 的 The Illustrated GPT-2本文从语言模型的基本介绍开始，以一种非常容易理解的方式逐步解释 GPT-2 模型。我强烈建议读者阅读这篇文章。

哈佛大学 The Annotated Transformer 使用 PyTorch 实现了完整的 transformer 架构，是深入理解 transformer 的好方法。

然后，让我们在这些优秀的现有资源的基础上，用代码实现 GPT-2 吧~

摘要

自然语言处理任务，如问答、机器翻译、阅读理解等，通常是在特定任务的数据集上进行有监督的学习。我们证明，当语言模型在一个名为 WebText 的数百万网页的新数据集上训练时，它开始学习这些任务，而不需要任何明确的监督。我们最大的模型，GPT-2，是一个 1.5B 参数的 transformer，它可以获得最先进的语言建模成果，但仍然不适合 WebText。模型中的示例反映了这些改进，并包含连贯的文本段落。这些发现为构建语言处理系统提供了一条有希望的途径，该系统可以从自然发生的演示中学习执行任务。

Zero-shot 设置是不微调语言模型并直接在目标数据集上运行推理的设置。例如，在 WebText 上预览一个 LM，并直接尝试预测 Amazon 影评数据集的下一个单词。

模型架构（GPT-2）

我们的 LM 使用基于 transformer 的架构。该模型主要遵循 OpenAI GPT 模型的细节，并进行了一些修改。层规范化被移动到每个子块的输入，类似于预激活剩余网络，并且在最终的自关注块之后添加了额外的层规范化。我们在初始化时将剩余层的权重按 1/√N 的因子进行缩放，其中 N 是剩余层的数量。词汇量扩大到 50257 个单词。我们还将上下文大小从 512 增加到 1024 个，并使用更大的批大小——512。

模型规格（GPT）

我们的模型基本上遵循了最初 transformer 的工作原理。我们训练了一个 12 层的只解码的 transformer，它有隐藏的自注意力头（768 维状态和 12 个注意力头）。对于位置前馈网络，我们使用了 3072 维的内部状态。我们使用 Adam 优化方案，最大学习速率为 2.5e-4。学习速率在前 2000 次更新中从零线性增加，并使用余弦调度将其退火为 0。我们在 64 个随机抽样的小批量、512 个令牌的连续序列上训练了 100 个阶段。由于 layernorm 在整个模型中广泛使用，简单的 N（0，0.02）权重初始化就足够了。我们使用了一个 bytepair 编码（BPE）词汇表。我们还采用了在中提出的 L2 正则化的改进版本，在所有非偏倚或增益权重上的 w=0.01。对于激活函数，我们使用高斯误差线性单位（GELU）。

导入

import torch

import copy

import torch.nn as nn

import torch.nn.functional as F

from torch.nn.modules import ModuleList

from torch.nn.modules.normalization import LayerNorm

import numpy as np

import os

from tqdm import tqdm_notebook, trange

import logging

logging.basicConfig(level = logging.INFO)

logger = logging.getLogger()

GPT-2 内部的 transformer 解码器

要重用用于描述 transformer 的术语，注意是一个查询（Q）和一组键（K）和值（V）对的函数。为了处理更长的序列，我们修改了 transformer 的多头自注意力机制，通过限制 Q 和 K 之间的点积来减少内存使用：

注意力是查询、键和值的组合

class Conv1D(nn.Module):

def __init__(self, nx, nf): super().__init__()

self.nf = nf

w = torch.empty(nx, nf)

nn.init.normal_(w, std=0.02)

self.weight = nn.Parameter(w)

self.bias = nn.Parameter(torch.zeros(nf))

def forward(self, x):

size_out = x.size()[:-1] + (self.nf,)

x = torch.addmm(self.bias, x.view(-1, x.size(-1)), self.weight)

x = x.view(*size_out)

return x

CONV1D 层解释

CONV1D 层本身可以看作是一个线性层。本质上，它是投射一个初始张量 x（最终尺寸为 x.size(-1)）并传递给它，最终尺寸为 self.nf。

下面是相同的输出示例：

d_model = 768

conv1d = Conv1D(d_model, d_model*3)

x = torch.rand(1,4,d_model) #represents a sequence of batch_size=1, seq_len=4 and embedding_sz=768, something like "Hello how are you"

x = conv1d(x)

x.shape

>> torch.Size([1, 4, 2304])

如上例所示，CONV1D 返回的张量的最终维数是初始大小的 3 倍。我们这样做是为了能够将输入转换为查询、键和值矩阵。

然后可以检索查询、键和值矩阵，如下所示：

query, key, value = x.split(d_model, dim=-1)

query.shape, key.shape, value.shape

>> (torch.Size([1, 4, 768]), torch.Size([1, 4, 768]), torch.Size([1, 4, 768]))

将输入转换为 Q、K 和 V 矩阵的另一种方法是必须有单独的 Wq、Wk 和 Wv 矩阵。我已经在这篇文章底部的附加部分解释了这一点。我发现这种方法更直观、更具相关性，但在本文中我们使用了 CONV1D 层，因为我们重用了 Hugging Face 的 CONV1D 预训练权重。

前向层解释

class FeedForward(nn.Module):

def __init__(self, dropout, d_model=768, nx=768*4):

super().__init__()

self.c_fc = Conv1D(d_model, nx)

self.c_proj = Conv1D(nx, d_model)

self.act = F.gelu

self.dropout = nn.Dropout(dropout)

def forward(self, x):

return self.dropout(self.c_proj(self.act(self.c_fc(x))))

在 Jay Alammar 的文章中有一个很好的解释，也就是上面提到的，输入是如何先经过注意力层，然后再进入前向层的。前馈网络是一个正常的网络，它接受来自注意力层（768）的输出，将其投射到 nx(768×4)维，添加一个激活函数 self.act(GELU)，将其投射回 d_model (768) 并添加 dropout(0.1)。

标度点产品注意力

我们称我们的注意力为「标度点产品注意力」。输入包括维度 dk 的查询和键以及维度 dv 的值。我们使用所有键计算查询的点积，用√dk除以每个键，然后应用 softmax 函数获得值的权重。

在实际应用中，我们同时计算一组查询的注意力函数，将它们组合成一个矩阵 Q，并将键和值组合成矩阵 K 和 V。我们将输出矩阵计算为：

输出矩阵为 Q、K 和 V 的组合

最常用的两个注意力函数是加性注意力函数和点积（乘法）力函数注意。除了比例因子 1/√dk 外，点积注意力与我们的算法相同。附加注意力使用具有单个隐藏层的前馈网络计算兼容性函数。虽然二者在理论复杂度上相似，但在实际应用中，点积注意力速度更快，空间效率更高，因为它可以使用高度优化的矩阵乘法码来实现。当 dk 值较小时，两种机制的表现相似，但在 dk 值较大时，加性注意力优于点积注意力。我们怀疑，对于 dk 的较大值，点积在数量上增长较大，将 softmax 函数推入具有极小梯度的区域。为了抵消这一影响，我们将网点产品缩放至 1/√dk。

为了在代码中实现注意力层，我们首先利用 CONV1D 层，得到前面解释的 Q、K 和 V 矩阵。

一旦我们有了 Q、K 和 V 矩阵，我们就可以使用函数 _attn 来执行注意力。此函数复制了上述注意力点积公式。

class Attention(nn.Module):

def __init__(self, d_model=768, n_head=12, n_ctx=1024, d_head=64, bias=True, scale=False):

super().__init__()

self.n_head = n_head

self.d_model = d_model

self.c_attn = Conv1D(d_model, d_model*3)

self.scale = scale

self.softmax = nn.Softmax(dim=-1)

self.register_buffer("bias", torch.tril(torch.ones(n_ctx, n_ctx)).view(1, 1, n_ctx, n_ctx))

self.dropout = nn.Dropout(0.1)

self.c_proj = Conv1D(d_model, d_model)

def split_heads(self, x):

"return shape [`batch`, `head`, `sequence`, `features`]"

new_shape = x.size()[:-1] + (self.n_head, x.size(-1)//self.n_head)

x = x.view(*new_shape)

return x.permute(0, 2, 1, 3)

def _attn(self, q, k, v, attn_mask=None):

scores = torch.matmul(q, k.transpose(-2, -1))

if self.scale: scores = scores/math.sqrt(v.size(-1))

nd, ns = scores.size(-2), scores.size(-1)

if attn_mask is not None: scores = scores + attn_mask

scores = self.softmax(scores)

scores = self.dropout(scores)

outputs = torch.matmul(scores, v)

return outputs

def merge_heads(self, x):

x = x.permute(0, 2, 1, 3).contiguous()

new_shape = x.size()[:-2] + (x.size(-2)*x.size(-1),)

return x.view(*new_shape)

def forward(self, x):

x = self.c_attn(x) #new `x` shape - `[1,3,2304]`

q, k, v = x.split(self.d_model, dim=2)

q, k, v = self.split_heads(q), self.split_heads(k), self.split_heads(v)

out = self._attn(q, k, v)

out = self.merge_heads(out)

out = self.c_proj(out)

return out

另一种实现注意力的方法在本博客底部的附加部分进行了说明。我发现它更直观，更容易与研究论文进行比较。它利用线性层而不是 CONV1D 将输入转换为 Q、K 和 V 矩阵。我们之所以没有使用它，是因为我们使用了预训练的权重，从 Hugging Face 转换为一维层。

多头注意力

下面一段是从论文「Attention is all you need」上摘取的。

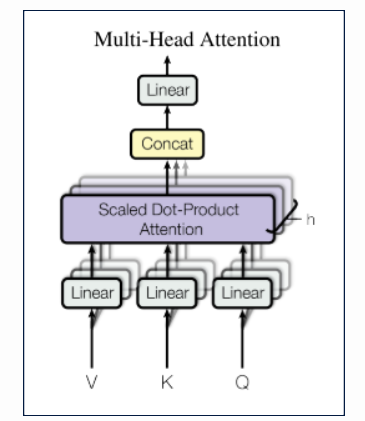
我们发现，使用不同的、学习到的线性映射将查询、键和值分别线性映射到 dk、dk 和 dv 维度更好。然后，在这些查询、键和值的隐射版本中，我们并行地执行注意力函数，生成 dv 维输出值。这些值被连接起来，然后再次进行映射，得到最终值，如下图所示：

多头注意力机制允许模型在不同的位置共同关注来自不同表示子空间的信息。

多头注意力等式

在这项工作中，我们使用了 h=8 个平行的注意力层，或者说头。其中，我们使用的都是 dk=dv=dmodel/h=64。由于每个头的维数减少，总的计算成本与全维度的单头部注意的计算成本相似。

不要被这个弄糊涂了，本质上，我们所做的就是给 Q，K 和 V 矩阵增加一个维数。也就是说，如果这些矩阵之前的大小是 [1, 4, 768]，表示 [bs, seq_len, d_model]，则这些矩阵被投影到[bs, n_head, seq_len, d_model//n_head]，大小为 [1, 12, 4, 64]。GPT-2 使用 12 个平行头。我们将 Q，K，V 矩阵分解到 split_heads 函数中。最后，当我们通过应用并行注意力得到一个输出时，我们将它连接到合并头中，返回到维度矩阵 [bs，seq_len，d_model]。

代码中的 GPT-2 模型体系结构

到目前为止，我们已经实现了多头注意和前馈层。如上图所示，这两层构成 transformer 解码器块的构建块。GPT-2 由 12 个 transformer 组组成。

这在 Jay Alammar 的文章中显示如下：

由 12 个解码块组成的 GPT 体系结构

transformer 解码器块说明

class TransformerBlock(nn.Module):

def __init__(self, d_model=768, n_head=12, dropout=0.1):

super(TransformerBlock, self).__init__()

self.attn = Attention(d_model=768, n_head=12, d_head=64, n_ctx=1024, bias=True, scale=False)

self.feedforward = FeedForward(dropout=0.1, d_model=768, nx=768*4)

self.ln_1 = LayerNorm(d_model)

self.ln_2 = LayerNorm(d_model)

def forward(self, x):

x = x + self.attn(self.ln_1(x))

x = x + self.feedforward(self.ln_2(x))

return x

transformer 组由注意力层和前馈层组成，如 GPT-2 架构模型规范所述：层规范化被移动到每个子块的输入，这里的子块是注意力和前馈。

因此，在 transformer 解码器块中，我们首先将输入传递给一个 LayerNorm，然后是第一个子注意力块。接下来，我们将这个子块的输出再次传递给 LayerNorm，最后传递给前馈层。

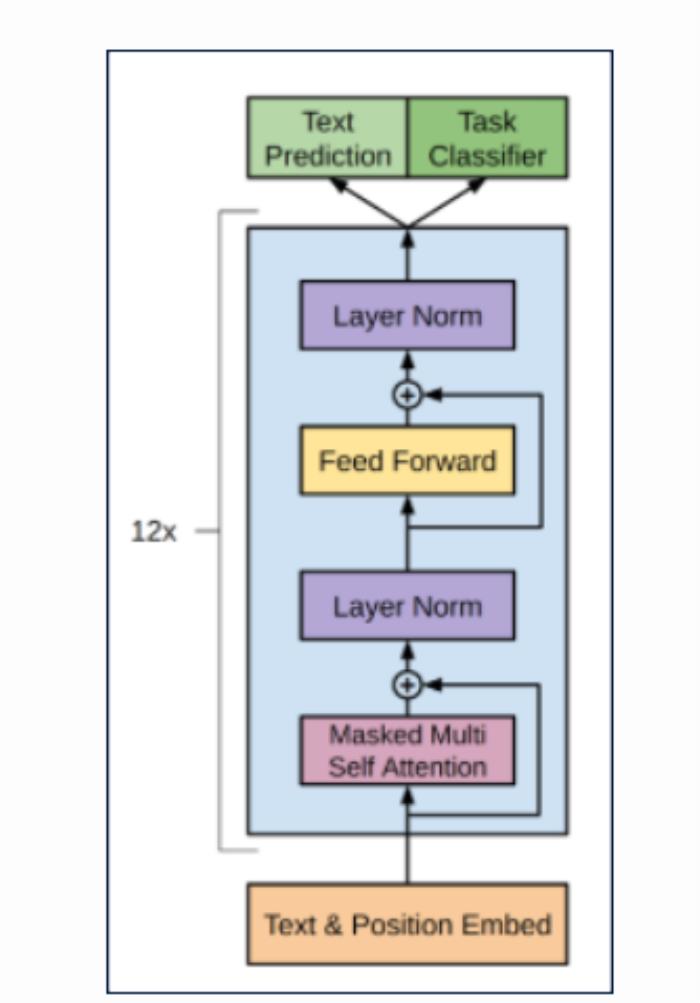
GPT-2架构说明

如 GPT 论文所述：我们训练了一个 12 层的只解码的 transformer，它有隐藏的自注意力头（768 个维度和 12 个注意力头）。

因此，完整的 GPT-2 体系结构是经过 12 次复制的 TransformerBlock。

def _get_clones(module, n):

return ModuleList([copy.deepcopy(module) for i in range(n)])

class GPT2(nn.Module):

def __init__(self, nlayers=12, n_ctx=1024, d_model=768, vcb_sz=50257):

super(GPT2, self).__init__()

self.nlayers = nlayers

block = TransformerBlock(d_model=768, n_head=12, dropout=0.1)

self.h = _get_clones(block, 12)

self.wte = nn.Embedding(vcb_sz, d_model)

self.wpe = nn.Embedding(n_ctx, d_model)

self.drop = nn.Dropout(0.1)

self.ln_f = LayerNorm(d_model)

self.out = nn.Linear(d_model, vcb_sz, bias=False)

self.loss_fn = nn.CrossEntropyLoss()

self.init_weights()

def init_weights(self):

self.out.weight = self.wte.weight

self.apply(self._init_weights)

def _init_weights(self, module):

if isinstance(module, (nn.Linear, nn.Embedding, Conv1D)):

module.weight.data.normal_(mean=0.0, std=0.02)

if isinstance(module, (nn.Linear, Conv1D)) and module.bias is not None:

module.bias.data.zero_()

elif isinstance(module, nn.LayerNorm):

module.bias.data.zero_()

module.weight.data.fill_(1.0)

def forward(self, src, labels=None, pos_ids=None):

if pos_ids is None: pos_ids = torch.arange(0, src.size(-1)).unsqueeze(0)

inp = self.drop((self.wte(src)+self.wpe(pos_ids)))

for i in range(self.nlayers): inp = self.h[i](inp)

inp = self.ln_f(inp)

logits = self.out(inp)

outputs = (logits,) + (inp,)

if labels is not None:

shift_logits = logits[..., :-1, :].contiguous()

shift_labels = labels[..., 1:].contiguous()

loss = self.loss_fn(shift_logits.view(-1, shift_logits.size(-1)), shift_labels.view(-1))

outputs = (loss,) + outputs

return outputs

return logits

我还没有提到的是位置编码和标记嵌入。因为，我们不能将诸如「hey」或「hello」之类的词直接传递给模型，所以我们首先将输入标记化。接下来，我们使用嵌入将标记表示为数字。Jay Alammar 的这篇文章很好地解释了嵌入。

此外，与按顺序传递输入词的 RNN 不同，transformer 并行地接受输入矩阵，从而失去了被输入词的位置感。为了弥补这一损失，在将标记嵌入处理到模型之前，我们添加了 Positional Encoding——一种指示序列中单词顺序的信号。如前所述，由于 GPT-2 的上下文大小是 1024，因此位置编码的维度是 [1024, 768]。

从[The Illustrated GPT-2]引用的位置编码

因此，GPT-2 体系结构的输入是通过一个 Dropout 的标记嵌入和位置编码的总和。一旦我们有了输入矩阵，我们就让其通过 GPT-2 架构的 12 层中的每一层，其中每一层都是一个由两个子层组成的 transformer 译码器块——注意力和前馈网络。

语言建模或分类

当使用 GPT-2 作为语言模型时，我们将输入传递到最终层形式，并通过最终大小为[768, vocab_sz]（50257）的线性层，得到大小为[1，4，50257]的输出。这个输出表示下一个词汇输入，我们现在可以很容易地通过一个 softmax 层，并使用 argmax 以最大的概率获得单词在词汇表中的位置。

对于分类任务，我们可以通过大小为 [768, n] 的线性层来传递从 GPT-2 架构接收到的输出，以获得每个类别的概率（其中 n 表示类别的数量），然后通过 softmax 传递，得到最高的预测类别，并使用 CrossEntropyLoss 来训练架构进行分类。

这就是 GPT-2 背后的全部魔法。它是一种基于解码器的 transformer 式结构，与 RNN 不同，它采用与位置编码并行的输入，通过 12 个 transformer 解码器层（由多头注意力和前馈网络组成）中的每一层来返回最终输出。

让我们在语言模型任务中看看这个模型的实际作用。

使用 Hugging Face 预训练权重生成示例文本

首先，让我们用 Hugging Face 提供的预训练权重初始化模型。

model = GPT2()

# load pretrained_weights from hugging face

# download file

model_dict = model.state_dict() #currently with random initialization

state_dict = torch.load("./gpt2-pytorch_model.bin") #pretrained weights

old_keys = []

new_keys = []

for key in state_dict.keys():

if "mlp" in key: #The hugging face state dict references the feedforward network as mlp, need to replace to `feedforward` be able to reuse these weights

new_key = key.replace("mlp", "feedforward")

new_keys.append(new_key)

old_keys.append(key)

for old_key, new_key in zip(old_keys, new_keys):

state_dict[new_key]=state_dict.pop(old_key)

pretrained_dict = {k: v for k, v in state_dict.items() if k in model_dict}

model_dict.update(pretrained_dict)

model.load_state_dict(model_dict)

model.eval() #model in inference mode as it's now initialized with pretrained weights

现在让我们生成文本。我们将使用 Hugging Face 的预训练标记器将单词转换为输入嵌入。

from transformers import GPT2Tokenizer

tokenizer = GPT2Tokenizer.from_pretrained("gpt2")

context = torch.tensor([tokenizer.encode("The planet earth")])

def generate(context, ntok=20):

for _ in range(ntok):

out = model(context)

logits = out[:, -1, :]

indices_to_remove = logits < torch.topk(logits, 10)[0][..., -1, None]

logits[indices_to_remove] = np.NINF

next_tok = torch.multinomial(F.softmax(logits, dim=-1), num_samples=1).squeeze(1)

context = torch.cat([context, next_tok.unsqueeze(-1)], dim=-1)

return context

out = generate(context, ntok=20)

tokenizer.decode(out[0])

>> 'The planet earth is the source of all of all the light," says the study that the government will'

附加内容

另一种实现注意力的方法，在 fast.ai 的 NLP 课程中有，我发现更直观的方法如下：

class Attention_FASTAI(nn.Module):

def __init__(self, d_model=768, n_head=12, d_head=64, n_ctx=1024, bias=True, scale=False):

super().__init__()

self.n_head = n_head

self.d_head = d_head

self.softmax = nn.Softmax(dim=-1)

self.scale = scale

self.atn_drop = nn.Dropout(0.1)

self.wq, self.wk, self.wv = [nn.Linear(d_model, n_head*d_head,

bias=bias) for o in range(3)]

def split_heads(self, x, layer, bs):

x = layer(x)

return x.view(bs, x.size(1), self.n_head, self.d_head).permute(0,2,1,3)

def _attn(self, q, k, v, attn_mask=None):

scores = torch.matmul(q, k.transpose(-2, -1))

if self.scale: scores = scores/math.sqrt(v.size(-1))

if attn_mask is not None:

scores = scores.float().masked_fill(attn_mask, -float('inf')).type_as(scores)

attn_prob = self.atn_drop(self.softmax(scores))

attn_vec = attn_prob @ v

return attn_vec

def merge_heads(self, x, bs, seq_len):

x = x.permute(0, 2, 1, 3).contiguous()

return x.view(bs, seq_len, -1)

def forward(self, q, k, v, mask=None):

bs, seq_len = q.size(0), q.size(1)

wq, wk, wv = map(lambda o:self.split_heads(*o, bs),

zip((q,k,v), (self.wq, self.wk, self.wv)))

attn_vec = self._attn(wq, wk, wv)

attn_vec = self.merge_heads(attn_vec, bs, seq_len)

return attn_vec

上面的实现与我们采用的实现方法的关键区别在于，这个实现没有使用 CONV1D，而是先将输入 x 传递给 self.wq、self.wk 和 self.wv 线性层，得到 wq、wk 和 wv 矩阵，然后接下来和前面一样。

写在最后

特别感谢 Hugging Face 创建了一个开源的 NLP 库，并提供了许多可使用的预训练模型。如前所述，本文中的代码直接来自 Hugging Face 库。The Illustrated GPT-2是关于 GPT-2 知识最全的博客之一。最后，Harvard NLP 的 The Annotated Transformer完成了一个很棒且易于学习的 PyTorch 中 Transformers 的实现。